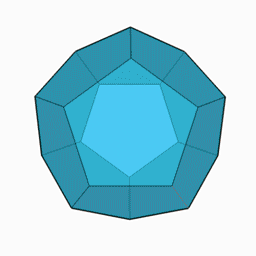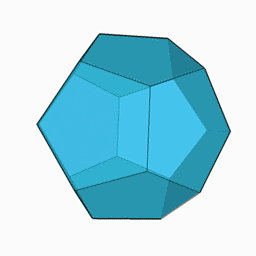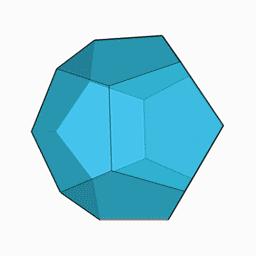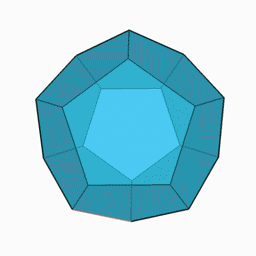
Regelmæssig dodecahedron

Regelmæssig dodecahedron


Type	Platonisk faststof
Ansigter	12 almindelige pentagoner
Kanter	30
Hjørner	20
Ansigter / toppunkt	3
Funktion	2

Schläfli-symbol	{5.3}
Wythoff symbol	3
Coxeter-Dynkin-diagram
Dobbelt	Icosahedron
Symmetri gruppe	Jeg h
Bind	${\ displaystyle {\ tfrac {15 + 7 {\ sqrt {5}}} {4}} a ^ {3}}$
Areal	${\ displaystyle 3 {\ sqrt {25 + 10 {\ sqrt {5}}}} a ^ {2}}$
Dihedral vinkel	arccos (-1 / √ 5 ) ( 116,565 05 ° )
Ejendomme	Konveks , regelmæssig

Den almindelige dodecahedron er en dodecahedron, hvis 12 ansigter er regelmæssige pentagoner . Den har 30 kanter og 20 hjørner . Det er en af de 5 faste stoffer i Platon . Den har en afgrænset kugle, der passerer gennem sine 20 hjørner, og en indskrevet kugle, der er tangent til dens 12 ansigter.

Da det har 5 hjørner pr. Ansigt og 3 ansigter pr. Hjørne, er dets Schläfli-symbol {5.3}.

Præfikset dodeca- , tolv på gammelgræsk , henviser til antallet af ansigter. Dens dobbelte polyhedron er den almindelige icosahedron .

Karakteristiske mængder

Hvis $a$ er længden af en kant:

radius på dens afgrænsede kugle er: hvor er det gyldne tal ; ${\ displaystyle R = {\ sqrt {3}} \; {\ frac {1 + {\ sqrt {5}}} {4}} \; a = {\ frac {\ sqrt {3}} {2}} \; \ varphi \; a}$ ${\ displaystyle \ varphi = {\ frac {1 + {\ sqrt {5}}} {2}}}$
dens område er :; ${\ displaystyle A = 3 {\ sqrt {25 + 10 {\ sqrt {5}}}} \; a ^ {2} = 3 {\ sqrt {5 (3 + 4 \ varphi)}} \; a ^ { 2}}$
dens volumen er :; ${\ displaystyle V = {\ frac {15 + 7 {\ sqrt {5}}} {4}} \; a ^ {3} = {\ frac {4 + 7 \ varphi} {2}} \; a ^ {3}}$
dens tovinklede vinkel (mellem to flader) er :; ${\ displaystyle \ arccos \ left (- {\ frac {1} {\ sqrt {5}}} \ right) = \ operatorname {arccot} \ left (- {\ frac {1} {2}} \ right) \ simeq 116 {,} 565 ^ {\ circ}}$
de 20 koordinatpunkter er hjørnerne i en almindelig dodecahedron centreret om oprindelsen og kanten . ${\ displaystyle \ left (0, \ pm {\ frac {1} {\ varphi}}, \ pm \ varphi \ right), \ quad \ left (\ pm {\ frac {1} {\ varphi}}, \ pm \ varphi, 0 \ right), \ quad \ left (\ pm \ varphi, 0, \ pm {\ frac {1} {\ varphi}} \ right), \ quad (\ pm 1, \ pm 1, \ pm 1)}$ ${\ displaystyle a = {\ frac {2} {\ varphi}}}$

Symmetrier

Dodecahedronen indrømmer et centrum for symmetri.

De isometrier forlader regelmæssig dodekaeder globalt invariant form, en gruppe . Denne gruppe indeholder:

akserotationer, der passerer gennem 2 modstående hjørner og med vinkel 2π / 3 eller 4π / 3 (120 ° og 240 °). Der er 10 par modstående hjørner, så 20 rotationer af denne type;
rotationerne af aksen, der passerer gennem midten af 2 modsatte flader og af vinklen 2π / 5, 4π / 5, 6π / 5 eller 8π / 5 (72 °, 144 °, 216 ° og 288 °). Da der er 6 par modstående flader, er der 24 rotationer af denne type;
rotationer af en vinkel π (180 °) omkring en akse gennem midten af 2 modsatte kanter (disse rotationer er også aksiale symmetrier). Der er 15 par med modsatte kanter, og derfor 15 rotationer af denne type;
symmetri med hensyn til dets centrum;
symmetrierne i forhold til et plan, der passerer gennem centrum og vinkelret på en af de 15 nævnte akser;
etc.

Med identiteten udgør de angivne 20 + 24 + 15-rotationer en undergruppe på 60 elementer, der er isomorfe til den alternerende gruppe A 5 . Enhver rotation tillader faktisk de fem kuber, der udgør dodecahedronen, og omvendt definerer enhver jævn permutation af de fem kuber en enkelt rotation.

Ligeledes identitet og symmetri s formular anden undergruppe betegnet C 2 .

Gruppen af isometrier, der er noteret, er produktet af dens to undergrupper; ${\ displaystyle I_ {h}}$

den indeholder 120 elementer.

Diverse egenskaber

Den regelmæssige dodecahedron og den regulære icosahedron er dobbelt fra hinanden, det vil sige, at polyhedronen, der for hjørner har centrum for den ene ansigt, er den anden.

Skelettet til den almindelige dodecahedron - sættet med dens hjørner forbundet med dets kanter - danner en graf kaldet en dodecahedron-graf .

Platon satte dodecahedronen i korrespondance med det hele, fordi det er det faste stof, der mest ligner sfæren. Aristoteles navngav dette femte element, aithêr ( ether på latin, "ether" på fransk) og postulerede, at universet var lavet af dette element, og at det var væsentligt for alle de andre, at det indeholdt dem alle.

Demonstration af eksistensen af et centrum for symmetri

Lad O være centrum for dodekaeder (punkt lige langt fra dets hjørner) og A et toppunkt. Linje OA skærer dodecahedronen ved et andet punkt K, som enten er centrum for et ansigt eller midtpunktet for en kant eller et toppunkt. Imidlertid omdanner de to rotationer af akse OA og de respektive vinkler 1/3 og 2/3 drejning dodekaederet i sig selv. K kan derfor kun være et toppunkt, og det symmetriske af toppunktet A med hensyn til O er toppunktet K.

Dodecahedronen indrømmer fem tripletter af ortogonale fly, der passerer gennem centrum, og som hver er et af symmetriplanerne for dodecahedronen.

Demonstration

Lad AB være en kant med midtpunktet M og KL den symmetriske kant af AB i forhold til centrum O.

Symmetrien i forhold til planet vinkelret på OM, der passerer gennem O, er produktet af rotation af en halv omdrejning af aksen OM ved symmetrien af centrum O.

Symmetrien S for aksen, der passerer gennem O og parallelt med AB, og som omdanner AB til LK, er en del af de 15 rotationer af gruppen H i en halv omdrejning, der bevarer dodecahedronen. Symmetrien i forhold til det plan, der passerer gennem O og vinkelret på AB, er produktet af S ved symmetrien med centrum O.

Symmetrien T for akse, der passerer gennem O og vinkelret på planet AOB, og som omdanner AB til KL, er en del af de 15 rotationer af gruppen H i en halv omdrejning, hvorved dodecahedronen bevares. Symmetrien med hensyn til planet, der passerer gennem AOB, er produktet af T ved symmetrien af centrum O

De tre ortogonale plan, der passerer gennem O, henholdsvis vinkelret på OM, til AB og til de to foregående, er derfor tre af de femten symmetriplaner for dodecahedronen. Ved fire rotationer af vinkler 1/5, 2/5, 3/5 og 4/5 af en drejning af den fælles akse med ansigtet indeholdende A og ikke indeholdende B opnår man fire andre tripletter af ortogonale symmetriplaner.

Konstruktion

1. Konstruktion af de første tre ansigter.

Lad ABCDE være en regelmæssig femkant, der udgør den første flade F1, med centrum O og kanten af længden a. I planet ABC skærer den vinkelrette på AB, der passerer gennem E linien OA i H. I planet, der passerer gennem OAH og vinkelret på planet ABC, skal G være et af de to skæringspunkter for den vinkelrette på planet i H med cirklen med centrum A og radius a. Punkt E og G er i samme plan vinkelret på AB og i samme afstand fra AB. Der er derfor en rotation med aksen AB, der omdanner E til G. Lad F3 være transformationen af F1 ved denne rotation: det er en regelmæssig femkant, der har den fælles kant AB med F1. Lad F2 være det symmetriske af F3 i forhold til OAG-planet: det er en almindelig femkant, der har den fælles kant AB med F1 og har den fælles kant AG med F3.

2. Konstruktion af følgende tre ansigter.

Lad R være rotation af aksen, der passerer gennem O og vinkelret på planet ABC og 1/5 af en omgang. Det omdanner ansigtet F2 til ansigtet F3, fordi flyene EAG og ABG danner den samme vinkel med planet ABC. Lad F4, F5 og F6 være transformationer af F2 af de respektive rotationer R 2 , R 3 og R 4 . F2 har en fælles kant med F3, så F6 har en fælles kant med R 4 (F3), som er lig med R 5 (F2) eller F2.

3. Konstruktion af de sidste seks ansigter.

Lad S være aksens rotation, der passerer gennem midten af ansigtet F2 og vinkelret på det, og med 1/5 omgang. Det omdanner henholdsvis ansigterne F1 og F3 til ansigterne F6 og F1, fordi planerne for F1, F3 og F6 danner den samme vinkel med planet for F2. Derudover har ansigtet F4 en fælles kant med F1 og en fælles kant med F3, men ingen fælles kant med F2. Dens transformation S (F4) har derfor en fælles kant med F6 og med F1, men ingen med F2: den er derfor F5.

Lad F7 og F8 være transformationerne af F1 af de respektive rotationer S 2 og S 3 . F1 har en kant fælles med F6, F8 har en kant fælles med F3.

Lad F9, F10 og F11 være transformationerne af F4 af de respektive rotationer S 2 , S 3 og S 4 . F4 har en kant, der er fælles med F5, og F11 har en kant, der er fælles med F4.

Kanten af F4 som ikke er fælles med nogen af de ti andre flader tidligere definerede, transformeres med S, S 2 , S 3 og S 4 i en kant henholdsvis F5, F9, F10, og F11, som er i en samme plan og danne en regelmæssig femkant, tolvte ansigt af dodecahedronen.

Anvendelser

Den middelalderlige digter Jean de Meung ( 1240 - 1305 ) beskrevet en divinatory brætspil , kaldet "dodechedron", som bruger en terning i form af en regulær dodekaeder, hver af de tolv ansigter især repræsenterer en af de tegn på Zodiac .

Den Megaminx er et puslespil afledt af Rubiks terning i form af en regulær dodekaeder.

Nogle rollespil på bordplader bruger 12-sidede terninger i deres spilsystem til actionopløsning. Disse 12-sidede terninger er dodecahedra.

Noter og referencer

Jean de Meung, Le dodechedron de fortune: en bog, der ikke er mindre behagelig og rekreativ, end subtil og genial mellem alle lykkenes spil og hobbyer , Nicolas Bonfons , Paris, 1577 .