Radian
| Radian | |
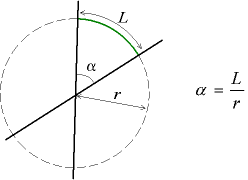 Definition af vinklen i radianer. | |
| Information | |
|---|---|
| System | Enheder afledt af det internationale system |
| Enhed af… | Planvinkel |
| Symbol | rad |
| Konverteringer | |
| 1 rad i ... | er lig med... |
| fuld tur | 2 π rad |
Den radian (symbol: rad ) er afledt af det internationale system , som måler plane vinkler . Selvom ordet " radian " blev opfundet i 1870'erne af Thomas Muir og James Thomson , har matematikere længe målt vinkler ved hjælp af forholdet mellem omkredsen og længden af radius som en enhed.
Definition
Overvej en vinkelsektor, der er dannet af to forskellige samtidige linjer , og en cirkel med radius r trukket i et plan indeholdende disse to linjer, hvis centrum er linjens skæringspunkt. Derefter er værdien af vinklen i radianer er forholdet mellem længden L af buen af en cirkel opfanget af linierne og radius r .
En vinkel på en radian aflytter på omkredsen af denne cirkel en bue med en længde svarende til radius. En fuld cirkel repræsenterer en vinkel på 2 π radianer, kaldet en fuld vinkel .
Brug af radianer er bydende nødvendigt, når man udleder eller integrerer en trigonometrisk funktion, eller endda når man bruger en begrænset udvikling af denne trigonometriske funktion: Faktisk kan vinklen findes i faktor, kun værdien i radianer har en retning. Beregningen af trigonometriske funktioner ved hjælp af en Taylor-serie antager derfor ekspressionen af vinklerne i radianer, ligesom anvendelsen af formlen til Euler , der udgjorde den ved at angive, at vinklerne skulle måles med længden i buens radius de opfanger mere end et århundrede før opfindelsen af udtrykket radian .
Små vinkler
For små vinkler udtrykt i radianer, sin x ≈ tan x ≈ x .
- For en vinkel på mindre end 0,17 radianer (dvs. ~ 10 °) er fejlen mindre end 1%;
- For en vinkel på mindre end 0,05 radianer (dvs. ~ 3 °) er fejlen mindre end 0,1%.
Inden for topografi , hvor vi beskæftiger os med svage vinkler, bruger vi vinkelmil , en praktisk enhed, defineret som den vinkel, der opfanges af en længde på 1 mm i en afstand på 1 m . Det bruges for eksempel til at bestemme afstanden fra en stav med kendt højde ved at måle dens tilsyneladende størrelse . Under de betingelser, hvor det tjener, identificeres denne enhed med en milliradian .
Forholdet mellem karakterer, grader og radianer
En fuld drejning er lig med 2 π radianer, 360 grader, 400 grader.
Derfor,
- En radian er cirka 57,3 ° eller 57 ° 18 '(360 ° ÷ 2π);
- en grad er cirka 17,5 milliradianer.
Konverteringsformlerne mellem grader og radianer er:
. .Konverteringsformlerne mellem kvaliteter og radianer er:
. .| vinkelnavn | værdi i radianer | værdi i karakterer | værdi i grader | værdi i sving |
|---|---|---|---|---|
| nul vinkel | 0 rad | 0 gon | 0 ° | 0 st |
| milliradian | 0,001 | 0,063 661 977 gon | 0 ° 3 ′ 26 ″ 16 ‴ eller 0,0573 ° | 0,00015915494 tr |
| π / 6 rad | 33,333 333 gon | 30 ° | 0,08333 st (1/12 st) | |
| π / 4 rad | 50 gon | 45 ° | 0,125 st (1/8 st) | |
| radian | 1 rad | 63,661,977 gon | 57 ° 17 ′ 44 ″ 48 ‴ | 0.1591549430919 st (1 / π / 2 st) |
| π / 3 rad | 66,666 666 gon | 60 ° | 0,1666 st (1/6 st) | |
| ret vinkel | π / 2 rad | 100 gon | 90 ° | 0,25 st |
| 2π / 3 rad | 133.333 333 gon | 120 ° | 0,333 st | |
| 3π / 4 rad | 150 gon | 135 ° | 0,375 omdr./min | |
| flad vinkel | π rad | 200 gon | 180 ° | 0,5 st |
| 5π / 4 rad | 250 gon | 225 ° | 0,625 st | |
| 3π / 2 rad | 300 gon | 270 ° | 0,75 omdr./min | |
| 7π / 4 rad | 350 gon | 315 ° | 0,875 omdr./min | |
| fuld vinkel | 2π rad | 400 gon | 360 ° | 1 st |
Se også
Bibliografi
- Richard Taillet, Loïc Villain og Pascal Febvre, Dictionary of Physics , Bruxelles, De Boeck ,2013, "Radian", s. 569
Relaterede artikler
Noter og referencer
- (in) AR Crathorne , " The Word" Radian " " , American Mathematical Monthly , bind. 19, n os 10-11,Oktober-november 1912, s. 166 ( DOI 10.2307 / 2971878 , JSTOR 2971878 ).
- (i) Robert J. Whitaker, " Hvorfra '' Radianen ''? " , The Physics Teacher (in) , bind. 32, nr . 7,Juni 1998, s. 444–445 ( DOI 10.1119 / 1.2344073 ).
- Taillet, Villain and Febvre 2013 , s. 39.



